Turning a sum of expectations into a single expectation with geometric series

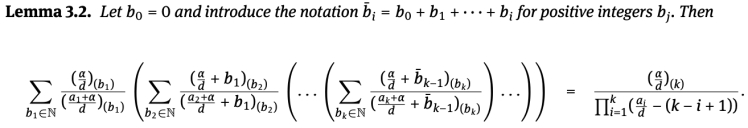
Screenshot 2020-01-07 at 17.11.07 — A technical lemma that is eager to learn how to turn a sum of expectations into a single expectation with geometric series.

At the dawn of 2020, in case anyone in the stat/ML community is not aware yet of Francis Bach’s blog started last year: this is a great place to learn about general tricks in machine learning explained with easy words. This month’s post The sum of a geometric series is all you need! shows how ubiquitous geometric series are in stochastic gradient descent, among others. In this post, I describe just another situation where the sum of a geometric series can be useful in statistics.

Turning a sum of expectations into a single expectation

I also found the sum of geometric series useful for turning a sum of expectations into a single expectation, by the linearity of expectation. More specifically, for a random variable $X$ compactly supported on $[-1,1]$ ,

$\sum_{k=1}^\infty \mathbb{E}[X^k] = \mathbb{E}\big[\sum_{k=1}^\infty X^k\big] = \mathbb{E}\big[\frac{X}{1-X}\big],$

where the sum can be infinite. Let us specify this with Beta variables: let $X\sim\text{Beta}(\alpha,\beta)$ with positive parameters $\alpha,\beta$ . Then the k-th moment of $X$ (for a positive integer $k$ ) is

$\mathbb{E}[X^k] = \frac{(\alpha)_k}{(\alpha+\beta)_k}$ ,

where $(\alpha)_k$ denotes the Pochhammer symbol, or rising factorial, $\alpha(\alpha+1)\ldots(\alpha+k-1)$ .

On the one hand, the sum $\sum_{k=1}^\infty \frac{(\alpha)_k}{(\alpha+\beta)_k}$ doesn’t look like an easy-going guy while turning it into a single expectation $\mathbb{E}\big[\frac{X}{1-X}\big]$ reveals a more amenable expression since we can use the result

$\mathbb{E}\big[X^a(1-X)^b\big] = \frac{B(\alpha+a,\beta+b)}{B(\alpha,\beta)}$

for any $a>-\alpha$ and $b>-\beta$ , and where $B$ denotes the beta function. We conclude that the required series has a finite limit for $\beta>1$ , in which case

$\sum_{k=1}^\infty \frac{(\alpha)_k}{(\alpha+\beta)_k} = \mathbb{E}\big[\frac{X}{1-X}\big] = \frac{B(\alpha+1, \beta-1)}{B(\alpha,\beta)}= \frac{\Gamma(\alpha+1)\Gamma(\beta)}{\Gamma(\alpha)\Gamma(\beta-1)}= \frac{\alpha}{\beta-1},$

which wasn’t trivial to me a priori.

Where I’ve used this trick

In a joint work with Caroline Lawless, who was an intern at Inria Grenoble Rhône-Alpes in 2018 (now Ph.D. candidate between Oxford and Paris-Dauphine), we have proposed a simple proof of Pitman-Yor’s Chinese restaurant process from its stick-breaking representation, thus generalizing a recent proof for the Dirichlet process by Jeff Miller. One of the technical lemmas there was the one provided in the top picture, that we proved by (backward) induction with the identity obtained in the above section.

By the way, the stick-breaking is a distribution over the infinite simplex, i.e. a specific way to randomly break a stick of unit length into infinitely many pieces, $p_1+p_2+p_3+\ldots = 1$ , with positive $p_i$ s, defined by $p_1 = v_1$ and $p_i = v_i\prod_{j<i}(1-v_j)$ for $i>1$ , where the $v_i$ s are iid beta random variable. Which sounds like a stochastic version of Zeno’s paradox $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\ldots = 1$ mentionned by Francis.