How to beat Monte Carlo (without QMC)

Say I want to approximate the integral

I(f) := \int_{[0, 1]^s} f(u) du

based on n evaluations of function f. I could use plain old Monte Carlo:

\hat{I}(f) = n^{-1}\sum_{i=1}^n f(U_i),\quad U_i\sim U([0, 1]^s).

whose RMSE (root mean square error) is O(n^{-1/2}).

Can I do better? That is, can I design an alternative estimator/algorithm, which performs n evaluations and returns a random output, with a RMSE that converges quicker?

Surprisingly (to me at least), the answer to this question has been known for a long time. If I am ready to focus on functions f\in\mathcal{C}^r([0, 1]^s), Bakhvalov (1959) showed that the best rate I can hope for is O(n^{-1/2-r/s}). That is, there exist algorithms that achieve this rate, and algorithms achieving a better rate simply do not exist.

Ok, but how can I actually design such an algorithm? The proof of Bakhvalov contains a simple recipe. Say I am able to construct a good approximation f_n of f, based on n evaluations; assume the approximation error is \|f-f_n\|_\infty = O(n^{-\alpha}), \alpha>0. Then I could compute the following estimator, based on a second batch of n evaluations:

\hat{I}(f) := I(f_n) + n^{-1} \sum_{i=1}^n (f-f_n)(U_i),\quad U_i\sim U([0, 1]^s).

and it is easy to check that this new estimator (based on 2n evaluations) is unbiased, that its variance is O(n^{-1-2\alpha}), and therefore its RMSE is O(n^{-1/2-\alpha}).

So there is strong connection between stochastic quadrature and function approximation. In fact, the best rate you can achieve for the latter is \alpha=r/s, which explains why the best rate you can get for the former is 1/2+r/s.

You can now better understand the “without QMC” in the title. QMC is about using points that are “better” than random points. But here I’m using IID points, and the improved rate comes from the fact I use a better approximation of f.

Here is a simple example of a good function approximation. Take s=1, and

f_n(u) = \sum_{i=1}^n f(\frac{2i-1}{2n}) 1_{[(i-1)/n, i/n]}(u)

that is, split [0, 1] into n intervals [(i-1)/n, i/n], and approximate f inside a given interval by its value at the centre of the interval. You can check that the approximation error is O(n^{-1}) provided f is C^1. So you get a simple recipe to obtain the optimal rate when s=1 and r=1.

Is it possible to generalise this type of construction to any r and any s? The answer is in our recent paper with Mathieu Gerber, which you can find here. You may also want to read Novak (2016), which is a very good entry on stochastic quadrature, and in particular gives a more detailed (and more rigorous!) overview of Bakhvalov’s and related results.

Also, please remind me not to try to type latex in wordpress ever again, it feels like this:

New smoothing algorithms in particles

Hi,
just a quick post to announce that particles now implements several of the smoothing algorithms introduced in our recent paper with Dang on the complexity of smoothing algorithms. Here is a plot that compares their running time for a given number of particles:

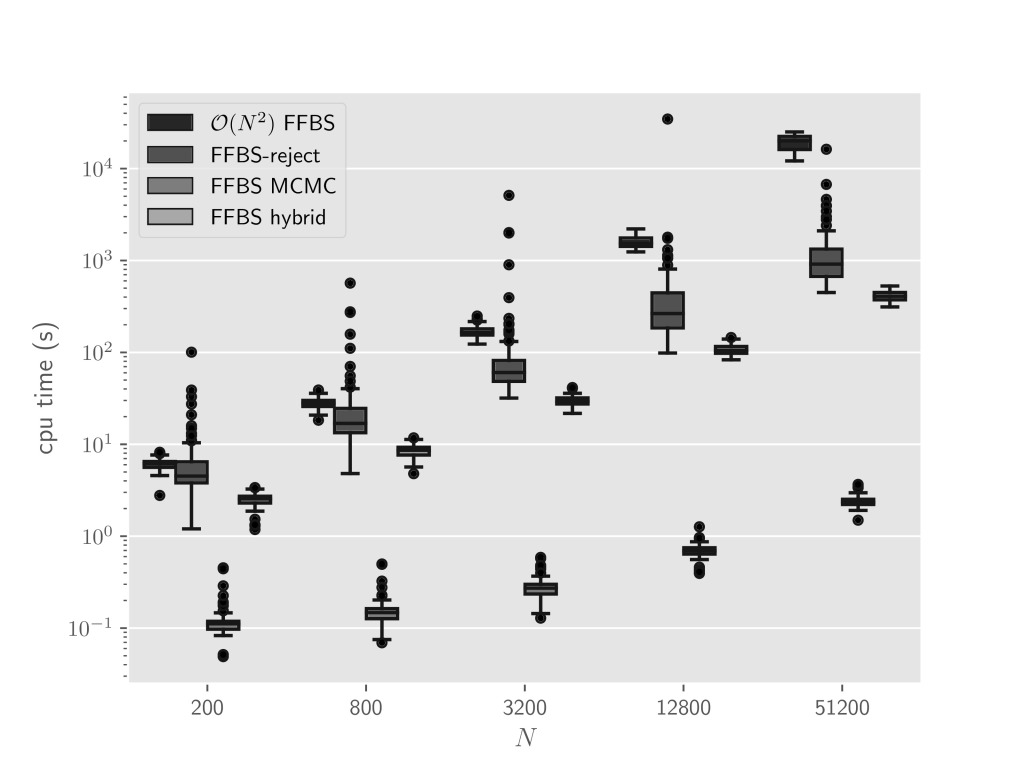
All these algorithms are based on FFBS (forward filtering backward smoothing). The first two are not new. O(N^2) FFBS is the classical FFBS algorithm, which as complexity O(N^2).

FFBS-reject uses (pure) rejection to choose the ancestors in the backward step. In our paper, we explain that the running time of FFBS-reject is random, and may have an infinite variance. Notice how big are the corresponding boxes, and the large number of outliers.

To alleviate this issue, we introduced two new FFBS algorithms; FFBS-hybrid tries to use rejection, but stops after N failed attempts (and then switch to the more extensive, exact method). FFBS-MCMC simply uses a (single) MCMC step.

Clearly, these two variants runs faster, but FFBS-MCMC wins the cake. This has to do with the inherent difficulty in implementing (efficiently) rejection sampling in Python. I will blog about that point later on (hopefully soon). Also, the running time of FFBS-MCMC is deterministic and is O(N).

That’s it. If you want to know more about these algorithms (and other smoothing algorithms), have a look at the paper. The script that generated the plot above is also available in particles (in folder papers/complexity_smoothing). This experiment was performed on the same model as the example as in the chapter on smoothing in the book, essentially. I should add that, in this experiment, the Monte Carlo variance of the output is essentially the same for the four algorithms (so comparing them only in terms of CPU time is fair).

particles 0.3: waste-free SMC, Fortran dependency removed, binary spaces

I have just released version 0.3 of particles (my Python Sequential Monte Carlo library). Here are the main changes:

No more Fortran dependency

Previous versions of particles relied on a bit of Fortran code to produce QMC (quasi-Monte Carlo) points. This code was automatically compiled during the installation. This was working fine for most users, but not all, unfortunately.

The latest (1.7) version of Scipy includes a stats.qmc sub-module. Particles 0.3 relies on this sub-module to generate QMC points, and thus is a pure Python package. This should mean fewer headaches when installing particles. Please let me know if this new version is indeed easier to install for you. Of course, make sure you have updated Scipy before installing particles; e.g. conda update scipy if you are using conda.

Waste-free SMC

With Dang, we wrote a paper on a new class of SMC samplers, waste-free SMC; see this paper on arxiv (to be published soon in JRSSB). In particular, the new version describes a particular scenario where it is possible to show formally that waste-free SMC >> standard SMC (in the sense of lower asymptotic variance).

The module smc_samplers now implements waste-free SMC by default (but standard SMC is still available, through option wastefree=False). Check the following notebook to see how to run an SMC sampler in particles.

SMC samplers for binary spaces

The new module binary_smc implements SMC samplers for binary spaces, i.e. {0, 1}^d, following Chopin and Schäfer (2014).

papers folder

The package now includes a folder called “papers”, which contains scripts that reproduce selected numerical experiments from previous papers:

  • scripts in sub-folder binarySMC reproduce most of the numerical experiments from Schäfer and Chopin (2014).
  • a script in sub-folder wastefreeSMC reproduces the first numerical experiment of Dau & Chopin (2020) on logistic regression. (See Dang’s github repo for the other experiments.)

Misc

  • Added a new resampling scheme, called killing (which may be traced to papers and work by Pierre del Moral).
  • Added a tutorial notebook on how to define non-trivial state-space models.

Comments / questions / poems ?

If you want to try particles, the first thing to read is the notebook tutorials. Second thing is to read the documentation of the respective modules. If you are still lost, feel free to raise an issue on github (or send me an e-mail, but github issues are more practical).

Online workshop: Measuring the quality of MCMC output

Yes, we need a better logo.

Hi all,

With Leah South from QUT we are organizing an online workshop on the topic of “Measuring the quality of MCMC output”. The event website is here with more info:

https://bayescomp-isba.github.io/measuringquality.html

This is part of ISBA BayesComp section’s efforts to organize activities while waiting for the next “big” in-person meeting, hopefully in 2023. The event benefits from the generous support of QUT Centre for Data Science. The event’s website will be regularly updated between now and the event in October 2021, with three live sessions:

  • 11am-2pm UTC on Wednesday 6th October,
  • 1pm-4pm UTC on Thursday 14th October,
  • 3pm-6pm UTC on Friday 22nd October.

Registration is free but compulsory (form here) as we want to make sure the live sessions remain convivial and focused; hence the rather specific theme, but it’s an exciting topic with lots of very much open questions, which we hope will attract both practitioners and methodologists. Meanwhile some material will be available on the website to everyone, including video recordings of presentations, and posters, so that the workshop hopefully benefits the wider community.

If you have suggestions for this event, or would like to organize a similar event in the future, on another “BayesComp” topic, do not hesitate to get in touch. Our contact details are on the workshop’s website.

Dempster’s analysis and donkeys

This post is about estimating the parameter of a Bernoulli distribution from observations, in the “Dempster” or “Dempster–Shafer” way, which is a generalization of Bayesian inference. I’ll recall what this approach is about, and describe a Gibbs sampler to perform the computation. Intriguingly the associated Markov chain happens to be equivalent to the so-called “donkey walk” (not this one), as pointed out by Guanyang Wang and Persi Diaconis.

Continue reading “Dempster’s analysis and donkeys”

particles 0.2: what’s new, what’s next (your comments most welcome)

I have just released version 0.2 of my SMC python library, particles. I list below the main changes, and discuss some ideas for the future of the library.

New module: variance_estimators

This module implements various variance estimators that may be computed from a single run of an SMC algorithm, à la Chan and Lai (2013) and Lee and Whiteley (2018). For more details, see this notebook.

New module: datasets

This module makes it easier to load the datasets included in the module. Here is a quick example:

from particles import datasets as dts

dataset = dts.Pima()
help(dataset) # basic info on dataset
help(dataset.preprocess) # how data was pre-processed
data = dataset.data # typically a numpy array

Performance improvements: multiprocessing

The library makes it possible to run several SMC algorithms in parallel, using the multiprocessing module. Hai-Dang Dau noticed there was some performance issue with the previous implementation (a few cores could stay idle) and fixed it.

While testing the new version, I noticed that function distinct_seeds (module utils), which, as the name suggests, generate distinct random seeds for the processes run in parallel, could be very slow in certain cases. I changed the way the seeds were generated to fix the problem (using stratified resampling). I will discuss this in more detail a separate blog post.

Plans for the future

Development of this library is partly driven by interactions with users. For instance, the next version will have a more general MvNormal distribution (allowing for a covariance matrix that varies across particles), because one colleague got in touch and needed that feature.

So don’t be shy, if you don’t see how to do something with particles, please get in touch. It’s likely our interaction will help me to either improve the documentation or add new, useful features. Of course, I also welcome direct contributions (through pull requests)!

Otherwise, I have several ideas for future releases, but, for the next one, it is likely I will focus on the following two areas.

SMC samplers

My priority #1 is to implement waste-free SMC in the package, following our recent paper with Dang. (Dang already has released his own implementation, which is built on top of particles, but, given that waste-free SMC seems to offer better performance than standard SMC samplers, it seems important to have it available in particles).

When this is done, I plan to add several important applications of SMC samplers, such as:

I also plan to document SMC samplers a bit better.

integration with Pytorch (or JAX, Tensorflow, etc)

Python libraries such as Tensorflow, Pytorch or JAX are all the rage in machine learning. They offer access to very fancy stuff, such as auto-differentation, and computation on the GPU.

I have started to play a bit with Pytorch, and even have a working implementation of a particle filter that runs entirely on the GPU. The idea is to make the core parts of particles completely independent of numpy. In that way, one may use Pytorch tensors to store the particles and their weights. This is really work in progress.

On the benefits of reviewing papers

Would you have agreed to review this paper if you had been asked?

When I’m asked by students whether they should accept some referee invitation (being it for a stat journal or a machine learning conference) I almost invariably say yes. I think that there is a lot to be learnt when refereeing papers and that this worth the time spent in the process. I’ll detail in this post why I think so.

First, this post is not about tips on how to write a referee report, but rather on why. It is instructive to consult tips on the hows, and good posts can be found out there. Note that some journals will also have specific guidelines.

Before diving into the benefits of refereeing, let me first say that a referee invitation can also be declined for many good reasons: in case of a conflict of interest (CoI), and/or if some of the authors are too close to you in some sense (although in some fields with a tiny community, this almost inevitably happens); if you do not feel qualified enough; or sometimes, if you feel you are qualified, but the refereeing task can seem overwhelming due to length or technicality of the paper; do not feel obliged to accept invitations from journals you do not know about, and of course ignore those coming from predatory journals or publishers (use this checklist). In any case, be conscious that it is ok to decline an invitation. Keep in mind that the associate editor in charge will very much appreciate pointers to alternative referee names.

Now, what are the benefits of refereeing? It is a legitimate question, given that refereeing work is usually time-consuming, done on a voluntary basis, without implying any direct or instant reward. So it is important to understand what you can gain out of it.

Learning about editorial process

In the early stages of an academic career, refereeing papers is an opportunity of learning by doing about the ins and outs of the editorial mechanism. You do not get the chance to practice replying to referee reports every other day when you are a student. But getting papers to review, you may also get to see replies by the authors, and reports from other referees (eg in revision rounds). This may help and build some habit about how you will get into action when your turn comes to reply to referees!

Opening research interests

We are usually asked to referee papers in our own area of expertise, but accepting to review papers slightly outside of one’s research interests can be rewarding. Be curious! There is a chance that reading submitted papers will trigger new research directions of yours. This happened to me at least twice: I have started to work on Bayesian deep learning after refereeing an ICLR paper dealing with the behaviour of neural networks in the infinitely wide limit; and (dis)proving a conjecture stated in a COLT submission stimulated a new line of research of mine on the sub-Gaussian property of random variables. Pay attention that in order to start working on such submitted papers in a legit way, you should ensure that they are also made available as preprints on some open repository like arxiv.

Prompting new opportunities

Refereeing papers surely increases your visibility. It is also a preliminary step before being associate editor. I’m AE for several stat journals, and managing papers is a task that I find enjoyable, with a social side that consists of writing referee invitation messages to colleagues. This helps connect or stay in touch with colleagues we do not have occasions to meet in conferences those days!

Everything You Always Wanted to Know About SMC, but were afraid to ask


Ever wanted to learn more about particle filters, sequential Monte Carlo, state-space/hidden Markov models, PMCMC (particle MCMC) , SMC samplers, and related topics?

In that case, you might want to check the following book from Omiros Papaspiliopoulos and I, which has just been released by Springer:

and which may be ordered from their web-site, or from your favourite book store.

The aim of the book is to cover the many facets of SMC: the algorithms, their practical uses in different areas, the underlying theory, how they may be implemented in practice, etc. Each chapter contains a “Python corner” which discusses the practical implementation of the covered methods in Python, a set of exercises, and bibliographical notes. Speaking of chapters, here is the table of contents:

  1. Introduction
  2. Introduction to state-space models
  3. Beyond state-space models
  4. Introduction to Markov processes
  5. Feynman-Kac models: definition, properties and recursions
  6. Finite state-spaces and hidden Markov models
  7. Linear-Gaussian state-space models
  8. Importance sampling
  9. Importance resampling
  10. Particle filtering
  11. Convergence and stability of particle filters
  12. Particle smoothing
  13. Sequential quasi-Monte Carlo
  14. Maximum likelihood estimation of state-space models
  15. Markov chain Monte Carlo
  16. Bayesian estimation of state-space models and particle MCMC
  17. SMC samplers
  18. SMC^2, sequential inference in state-space models
  19. Advanced topics and open problems

And here is one fancy plot taken from the book. (For some explanation, you will have to read it!)

A big thanks to all the colleagues who took the time to read draft versions and send feedback (see the introduction for a list of names). Also, don’t write books, folks. Seriously, it takes WAY too much time…